Дополнение

Сложносочиненное предложение

Сложносочиненным (ССП) называют сложное предложение, имеющее два и более независимых простых предложений в составе. Это значит, что их можно разбить точкой, при этом смысл не потеряется.

Части таких сложных предложений связаны союзами и союзными словами: соединительными (и, да, также и т. д.), противительными (а, но, зато и т. д.), разделительными (либо, то… то, не то… не то и т. д.) или их комбинациями.

Примеры:

• Хотелось пирога, и яблоки уже созрели.

• Хотелось пирога, но яблоки еще не созрели.

• То мать пирогов напечет, то бабушка с булочками приедет.

Иногда части сложносочиненных предложений связаны без сочинительного союза и союзного слова — по смыслу. Такие предложения называют бессоюзными.

Пример:

Лето заканчивалось лихо: на улице резко похолодало, листья начали алеть и чахнуть.

Знаки препинания в сложносочиненных предложениях

В предложениях с союзами и, да, однако, либо и т.д. принято ставить запятую. Кроме случаев, когда:

Исключение
Если у частей сложного предложения есть общий второстепенный член или придаточное, но их соединяет повторяющийся союз, нужно ставить запятую.

Пример:

На ярмарке в городе показывали кукольные представления, и торговцы продавали сахарную вату, и зазывалы кричали приглашения на аттракционы.

В бессоюзных сложносочиненных предложениях части делятся не только запятыми, но и тире, двоеточиями и точкой с запятой. Эту тему мы подробно разобрали в статье о сложносочиненных предложениях.

Выделение устойчивого выражения

В предыдущих примерах мы преобразовывали разные виды показательных уравнений путем разложения многочленов на множители, потому что хотели найти способ решения — получить одинаковые основания или выделить переменную, которую можно заменить. Так вот, когда мы выносим некий множитель за скобку или заменяем переменную, пытаясь упростить уравнение — это действие по сути и является выделением устойчивого выражения.

Устойчивое выражение — это некий многочлен, содержащий переменную, который в скрытом виде присутствует во всех показательных функциях уравнения. Его можно вынести за скобки или обозначить новой переменной, чтобы упростить уравнение.

Хорошая новость: так или иначе устойчивое выражение можно найти почти в любом трудном уравнении. Проблема только в том, чтобы научиться верно определять такое выражение, а этот навык появляется лишь с опытом.

Пример 1

3х+1 + 3х — 3х-2 = 35

В данном случае в качестве устойчивого выражения удобно взять 3х-2 как степень с наименьшим показателем. В итоге мы получим:

3х-2(33 + 32 — 1) = 35

3х-2 × 35 = 35

3х-2 = 1

Поскольку 1 равняется любое число в нулевой степени, мы можем записать:

3х-2 = 3

х — 2 = 0

х = 2

Пример 2

5 × 3-3х+1 + 3-3х+2 = 24

Для начала мы попробуем в левой части уравнения получить одинаковую степень: 3-3х+2 = 3-3х+1+1 = 3 × 3-3х+1.

Теперь у нас есть устойчивое выражение 3-3х+1, которое можно вынести за скобки, чтобы получить более простое уравнение:

3-3х+1(5+3) = 24

8 × 3-3х+1 = 24

3-3х+1 = 31

-3х + 1 = 1

х = 0

Сложение и умножение вероятностей

Немного теории:

• Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В можно записать так: A ⊂ B.
• События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается так: А = В.
• Суммой событий А и В называется событие А + В, которое наступает тогда, когда наступает хотя бы одно из событий: А или В.

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

Если случайные события A₁, A₂,…, A_n образуют полную группу несовместных событий, то справедливо равенство: 

P(A1) + P(A2) + … + P(An) = 1. Такие события (гипотезы) используют при решении задач на полную вероятность.

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

1. только в одном справочнике;
2. только в двух справочниках;
3. во всех трех справочниках.

Как рассуждаем:

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Рациональные уравнения

Рациональные уравнения широко применяются в приборостроении, космических исследованиях, финансовых операциях и т.д.

Подобие фигур широко применяется в измерительных, конструкторских и дизайнерских работах.

Это интересно!

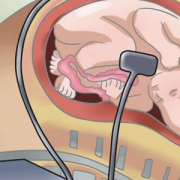
На рисунке изображена модель орбитального космического корабля, предназначенная для полёта в космос туристов. Корабль рассчитан на 6 пассажиров и 2 членов экипажа.

Для того, чтобы рассчитать оптимальные размеры корабля конструкторам и инженерам пришлось решить много рациональных уравнений.

Рациональные уравнения

Уравнение, содержащее в левой и правой части рациональные выражения называется рациональным уравнением. Во многих задачах приходится решать рациональные уравнения, содержащие переменную в знаменателе. В этом случае необходимо указывать область допустимых значений переменных (ОДЗ).

Пример:

В данном уравнении ОДЗ Учитывая, что умножим обе части уравнения на

отсюда получим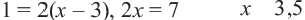

Подставим полученное значение в уравнение:

Таким образом, является корнем уравнения. Данное уравнение не имеет других корней.

Пример:

Решим уравнение

ОДЗ данного уравнения Умножим обе части уравнения на общий

знаменатель

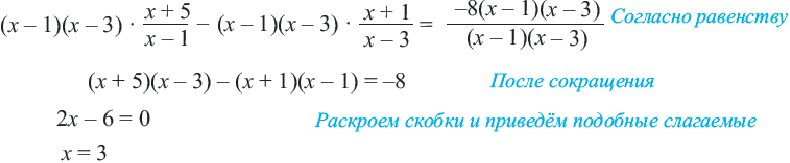
Пример:

В уравнении, ОДЗ

Используя свойство пропорции можно написать:

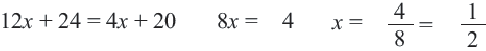
Пример:

Решим уравнение. Здесь ОДЗ,

Умножим обе части уравнения на

Отсюда

Проверьте, являются ли оба этих числа корнями данного уравнения.

Пример:

Решим уравнение

Запишем уравнение в виде и умножим обе стороны на общий множитель Получим

Отсюда

При проверке, убеждаемся что, не удовлетворяет уравнению, т.к. превращает знаменатель в «0». Таким образом, корнем данного уравнения является только

Внимание! После решения рационального уравнения, содержащего переменную в знаменателе, нужно обязательно выполнить проверку корней

Решение задач с помощью рациональных уравнений

Задачи на работу

Задача. Двое рабочих могут выполнить некоторую работу за 12 дней. За сколько дней каждый рабочий выполнит эту работу в отдельности, если одному из них для выполнения этой работы потребуется на 10 дней больше ,чем другому? Решение: Пусть, 2-ой рабочий может выполнить работу за дней, тогда 1-ый рабочий выполнит её за дней

Первый рабочий за 1 день выполняет — ую часть работы, 2-ой — — ую. Вместе, за 1 день они выполнят часть работы. Зная, что вместе за 1 день они выполняют часть работы (согласно условию), составим уравнение Умножим обе части уравнения на Получим, 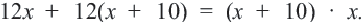После упрощения имеем Решением данного уравнения являются числа и (не удовлетворяет условию, т.к. ). Итак Ответ: 2-ой рабочий выполняет работу за 20 дней, а 1-ый — за 30 дней.

Задачи на движение

Задача. Путь длиной 480 км проходит по асфальтовой и по просёлочной дороге. Автомобиль расстояние 80 км по просёлочной дороге, прошёл со скоростью на 40 км/час меньше, чем по асфальтовой дороге. Зная, что на весь путь он затратил 7 часов, найдите время, которое потратил автомобиль при движении по просёлочной дороге.

1-й способ:

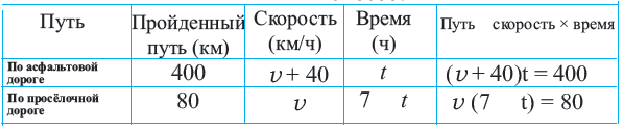Из 2-ой строки таблицы: 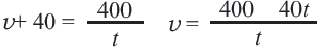Из 3-е1 строки таблицы: Отсюда получаем рациональное уравнение

Разделим обе части уравнения на 40:

Получим 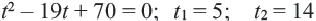(противоречит условию задачи)

Ответ: по просёлочной дороге 2 часа

2-ой способ: Автомобиль ехал по дороге, покрытой асфальтом часов, а по проселочной дороге часов.

Зная, что на весь путь он потратил 7 часов, составим уравнение:

Решив данное уравнение, получим = 40 км/ч. Тогда по просёлочной дороге он двигался 80 : 40 = 2 часа.

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Рациональные неравенства и их системы
• Геометрические задачи и методы их решения
• Прямые и плоскости в пространстве
• Интеграл и его применение
• Параллельность в пространстве
• Перпендикулярность в пространстве
• Векторы и координаты в пространстве
• Множества

Геометрия в пространстве (стереометрия)

Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара:

Площадь поверхности шара (или, другими словами, площадь сферы):

Как определить разряд прилагательного?

Задания, в которых нужно указать разряды имен прилагательных, встречаются, начиная с 6 класса. Самый простой алгоритм для этого выглядит так:

1. Определите, на какой вопрос отвечает прилагательное. Если это вопрос «чей?» — речь идет о притяжательном. Если же вопрос «какой?» — у нас есть выбор между двумя разрядами по значению: качественным и относительным.

2. Попробуйте образовать превосходную форму или добавить слово «очень». Если получилось — это, скорее всего, качественное прилагательное. Если нет — относительное.

Для относительных прилагательных есть и еще одна хитрость: если в слове нет суффикса, оно принадлежит именно этому разряду. Например: толстый, быстрый, теплый.

Попробуем определить разряд прилагательного на примере. Допустим, у нас есть предложение:

На завтрак был бабушкин яблочный пирог и ароматный чай.

У нас есть три прилагательных: бабушкин, яблочный и ароматный. Зададим вопросы:

• Бабушкин — чей?
• Яблочный — какой?
• Ароматный — какой?

Существует только один разряд по значению, связанный с вопросом «чей?». Мы можем сделать однозначный вывод:

бабушкин — притяжательное прилагательное.

От оставшихся двух попробуем образовать превосходную и краткую форму:

• самый яблочный — звучит не очень гармонично,
• самый ароматный, ароматнейший — звучит хорошо.

Краткая форма тоже есть только у одного прилагательного (ароматен).

Следовательно:

ароматный — качественное прилагательное.

О яблочном пироге мы можем сказать, что он сделан из яблок, т. е. в значении этого прилагательного есть сведения о том, как оно относится к другому предмету или явлению. Делаем вывод:

яблочный — относительное прилагательное.

Определение показательных неравенств

Показательными считаются неравенства, которые включают в себя показательную функцию. Другими словами, это неравенства с переменной в показателе степени: af(x) > ag(x), af(x) < ag(x). Из них показательно-степенными неравенствами являются те, в которых есть переменные и в показателе степени, и в основании.

Для изучения этой темы стоит повторить:

• показательные уравнения;
• метод интервалов;
• разложение многочлена на множители;
• свойства степенной функции.

И, конечно, для решения тригонометрических и логарифмических показательных неравенств также придется вспомнить формулы соответствующих разделов алгебры.

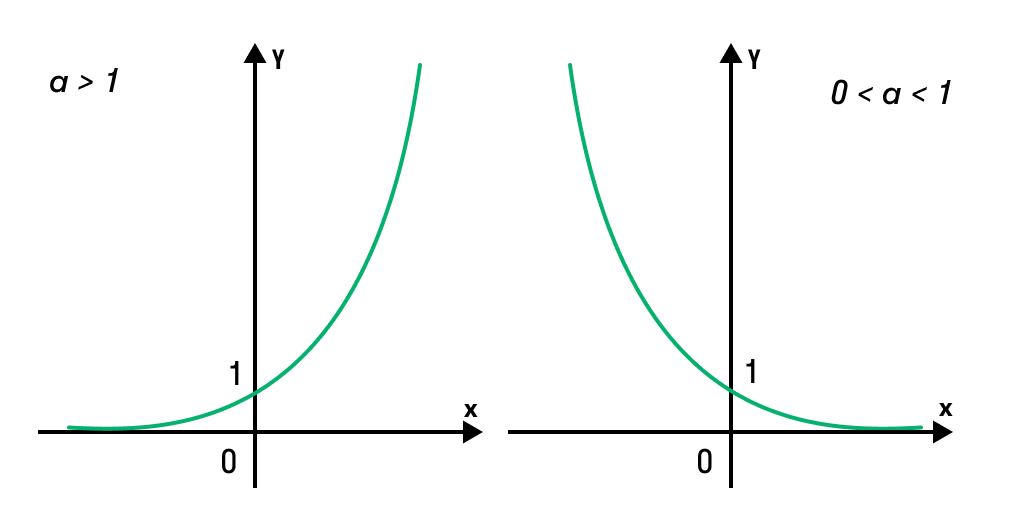
Если все это еще свежо в памяти, давайте приступим. Как и к показательным уравнениям, к неравенствам стоит подходить, помня о свойствах показательной функции. Напомним, что она выглядит так: y = ax, где a > 0 и a ≠ 1. Два графика ниже дают представление о том, на что похожа такая функция, когда основание степени а больше и меньше единицы. Наверняка вы уже догадались, каково главное свойство этой функции. Да, она монотонна.

При этом заметьте — значения а всегда больше нуля. На практике в этом несложно убедиться, если возводить какое-либо число во всевозможные степени, включая отрицательные. Например: 2-2 = 4, 2-4 = 1/16 и т. д. Значение функции будет уменьшаться, но никогда не достигнет нуля.

Для любых а и х верно неравенство ax > 0, т. е. показательная функция не принимает отрицательных значений.

Запишем следствие монотонности показательной функции в виде формул:

• af(x) > ag(x) <-> f(x) > g (x), когда функция возрастает, т. е. а > 1;
• af(x) > ag(x) <-> f(x) < g (x), когда функция убывает, т. е. 0 < а < 1.

На этом свойстве показательных неравенств так или иначе основываются все методы решения, и сейчас мы разберемся, как им пользоваться.

Понятие однородных членов предложения

Впервые тему однородных членов предложения школьники проходят в 3 классе и постепенно углубляют свои знания до 8 класса. Начнем с определения: узнаем, что значит «однородные члены предложения» и перейдем к нюансам.

Однородные члены (далее — ОЧ) — это члены предложения, которые выполняют одну и ту же синтаксическую функцию. Проще говоря, все они отвечают на один вопрос и связаны с одним и тем же словом в предложении.

Правило звучит так. Если два или более члена предложения относятся к одному и тому же слову, отвечают на один и тот же вопрос, являются одним и тем же членом предложения, то они являются однородными членами предложения.

Однородными членами может быть любая самостоятельная часть речи:

Составное сказуемое

Составное сказуемое называется так потому, что состоит из двух слов. Есть два вида составного сказуемого – глагольное и именное .

Составная глагольная форма

Включает вспомогательный глагол и глагол в инфинитиве (неопределенной формы).

Днём начал идти мелкий, колючий снег и продолжал сыпать до вечера. Вспомогательные глаголы здесь – «начал» и «продолжал» , они обозначают, что действие началось и продолжилось. Глаголы «идти» , «сыпать» означают собственно действие.

Как вспомогательный глагол используют:

1. Глаголы с обозначением начала, продолжения или завершения действия.
   • Начать, приниматься, стать – начало действия .
   • Продолжить – продолжение действия .
   • Перестать, прекратить, закончить – завершение действия .

1. Глаголы со значением намерения, желания, волеизъявления.

1. Глаголы, выражающие эмоции действующего лица.

1. Краткие прилагательные, которые не имеют полной формы.

Важно! Отличайте составное глагольное сказуемое от ПГС и глагола неопределенной формы, как второстепенного члена предложения. Гости пошли в сад (с какой целью?) посмотреть на прекрасные цветущие яблони

Пример демонстрирует нам как инфинитив глагола выступает в качестве дополнения

Гости пошли в сад (с какой целью?) посмотреть на прекрасные цветущие яблони . Пример демонстрирует нам как инфинитив глагола выступает в качестве дополнения.

Составная именная форма

Складывается из вспомогательного глагола и второго слова, которое выражено другой частью речи. В качестве таких могут выступать:

1. Имена существительные именительного или творительного падежа.

1. Прилагательные в полной или краткой форме, в формах сравнительных степеней.

1. Местоимения.

1. Числительные, или числительные + существительные.

1. Полные или краткие причастия.

Отрицательное предложение. Примеры предложений:

С обычными глаголами

В английском языке, чтобы построить отрицательное предложение в Present Simple, нужны вспомогательные глаголы do и does. Они ставятся перед основным глаголом вместе с частицей not. Примеры:

• I work (я работаю) – I do not work (я не работаю).
• He reads (он читает) – He does not read (он не читает).

Когда употреблять do, а когда does?

Очень просто! Does используется с 3-м лицом ед.ч. (местоимениями he, she, it), а do – со всеми остальными.

Do not и does not очень часто сокращаются в разговорном английском. Do not имеет форму don’t, а does not – doesn’t.

Примеры отрицательных предложений в Present Simple с обычными глаголами:

Полная форма	Сокращенная форма	Перевод
I do not live in Moscow.	I don’t live in Moscow.	Я не живу в Москве.
He does not wear T-shirts.	He doesn’t wear T-shirts.	Он не носит футболки.
She does not play computer games.	She doesn’t play computer games.	Она не играет в компьютерные игры.
It does not look good.	It doesn’t look good.	Это не выглядит хорошо.
You do not like chocolate.	You don’t like chocolate.	Ты не любишь шоколад. / Вы не любите шоколад.
We do not go to the hospital.	We don’t go to the hospital.	Мы не ходим в больницу.
They do not buy books.	They don’t buy books.	Они не покупают книги.
Mike does not take music lessons.	Mike doesn’t take music lessons.	Майк не берет уроки музыки.
Kate and Jane do not argue.	Kate and Jane don’t argue.	Кейт и Джейн не ссорятся.
Vegetarians do not eat meat.	Vegetarians don’t eat meat.	Вегетарианцы не едят мясо.

С глаголом to be

Отрицания с глаголом to be образуются проще, чем с обычными глаголами. Мы просто добавляем частицу not после am, is, are. Примеры:

• I am a student (Я студент) – I am not a student (Я не студент).
• He is in Australia (Он в Австралии) – He is not in Australia (Он не в Австралии).

В разговорной речи отрицание с to be очень часто сокращается. Однако, у сочетания am not есть только один вариант сокращения. Примеры:

I am not sad. – I‘m not sad.

У сочетаний is not и are not есть два варианта сокращений. Примеры:

• He is not at school. – He isn’t at school / He‘s not at school.
• We are not cousins. – We aren’t cousins. / We‘re not cousins. 

Примеры отрицательных предложений в Present Simple с глаголом to be:

Полная форма	Сокращенная форма	Перевод
I am not a writer.	I’m not a writer.	Я не писатель.
He is not in the garden.	He isn’t in the garden.	Он не в саду.
She is not a cook.	She isn’t a cook.	Она не повар.
It is not on the table.	It isn’t on the table.	Это не на столе.
We are not Irish.	We aren’t Irish.	Мы не ирландцы.
They are not tired.	They aren’t tired.	Они не устали.
You are not responsible.	You aren’t responsible.	Ты не ответственный. / Вы не ответственные.
The car is not in the garage.	The car isn’t in the garage.	Машина не в гараже.
The lessons are not canceled.	The lessons aren’t canceled.	Уроки не отменены.
The UK is not very large.	The UK isn’t very large.	Великобритания не очень большая.

Переместительный закон сложения

Начнем изучать основные законы математики со сложения натуральных чисел.

Переместительный закон сложения От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так: m + n = n + m

Переместительный закон сложения работает для любых чисел.

Если прибавить шестерку к двойке — получим восьмерку. И наоборот, прибавим двойку к шестерке — снова получим восьмерку. Это доказывает справедливость переместительного закона сложения.

• 6 + 2 = 8
• 2 + 6 = 8

Приведем пример с весами, которые используют продавцы в магазинах.

Если мы положим на одну чашу весов 3 килограмма конфет, а на другую — такие же 3 килограмма конфет, то стрелка весов будет на нейтральной позиции. Это говорит нам о том, что чаши действительно весят одинаково.

При этом неважно, как будут лежать конфеты, в каком порядке. Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма

От перестановки мест конфет их сумма, то есть вес, не меняется.

Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:

• 8 + 2 = 2 + 8
• 10 = 10

Формула переместительного закона для обыкновенных дробей:

Чтобы сложить две дроби нужно сложить числители, а знаменатель оставить прежним. Вот так:

Способы определения однородных членов предложения

Давайте разберемся, как найти однородные члены предложения.

Алгоритм определения однородных членов предложения:

1. Определить главные и второстепенные члены предложения. Отметить подлежащее и сказуемое;

2. Установить, есть ли в предложении члены, которые отвечают на один и тот же вопрос и относятся к одному и тому же слову;

3. Определить, какой связью они связаны:

   • сочинительной, которая выражена союзами,

   • бессоюзной, которая выражена с помощью перечислительной интонации.

Примеры:

Я выбрала букет из белых, розовых и зеленых хризантем.
Хризантем (каких?) белых, розовых и зеленых — однородные определения, так как они отвечают на один вопрос, относятся к одному слову (хризантем) и связаны сочинительной связью (сочинительный союз и).

В предложении может быть несколько однородных членов:

Артем и Маша много смеялись, пели и танцевали.
Артем и Маша — однородные подлежащие; смеялись, пели и танцевали — однородные сказуемые.

Теперь мы знаем, как определить однородные члены предложения.

А сейчас расскажем, какие члены предложения не являются однородными.

Если члены предложения относятся к одному и тому же слову, но отвечают на разные вопросы — их нельзя назвать однородными:

Я приду в гости завтра.
Я приду (куда?) в гости (когда?) завтра.
Обстоятельства относятся к сказуемому «приду», но отвечают на разные вопросы, поэтому их нельзя назвать однородными.

Однородными членами предложения не являются Повторяющиеся слова, которые выступают в роли единого члена предложения: мы точно плавали в воздухе и кружились, кружились, кружились. Повторяющиеся одинаковые формы, соединенные частицей «не», «так»: хочешь не хочешь; гулять так гулять. Сочетания двух глаголов, из которых первый лексически неполный: возьму и закричу; пойду переверну. Устойчивые сочетания с двойными союзами без запятой между ними: ни взад ни вперёд; ни за что ни про что; ни сном ни духом; и смех и грех; и так и сяк. Уточняющие члены предложения, которые отвечают на вопросы «где именно?», «как именно?», «кто именно?» и произносятся с интонацией обособления. Часто в их роли выступают обстоятельства времени и места: Я мечтаю побывать на Эльбрусе, на Кавказе. Побывать (где?) на Эльбрусе, на Кавказе — не однородные обстоятельства. На Кавказе — уточняющее обстоятельство, которое объясняет, где именно находится Эльбрус.

Переход прилагательных из одного разряда в другой

Существуют спорные прилагательные, которые формально по всем признакам относятся к одному разряду, но по значению больше тяготеют к другому. Так бывает, когда слово употребляется в переносном смысле, и в этом случае мы говорим о переходе из одного разряда в другой.

Сравните:

• золотое колье — сделанное из золота,
• золотой человек — очень хороший, доброжелательный.

Здесь мы видим переход в разряд качественных прилагательных из разряда относительных.

• Медвежья берлога — чья?
• Медвежья услуга — какая?
• Лисья нора — чья?
• Лисья хитрость — какая?

В данном случае мы видим переход из притяжательных в качественные. Такие явления характерны для всех трех разрядов прилагательных.

Переходить в другой разряд могут не только слова, которые употребляются в переносном значении. Также это бывает в ситуациях, когда речь идет о предметах из натуральной шерсти, меха:

• Беличья кладовая — чья?
• Беличья шуба — какая?

В первом случае речь о кладовой, принадлежащей белке, а значит, «беличья» — притяжательное прилагательное. Во втором же словосочетании шуба выполнена из меха белки, т. е. «беличья» — относительное прилагательное.

Существительное с предлогом «на пример»

Учитель указал на пример, приведенный в энциклопедии.

Зададим вопрос: указал на что? На пример.

«Пример» в данном случае – дополнение, выраженное именем существительным. Глагол-сказуемое управляет дополнением в форме винительного падежа единственного числа. Раздельное написание существительного с предлогом можно доказать при помощи падежного вопроса или определения между ними:

• на какой? при­мер;
• на чей? при­мер;
• на хоро­ший при­мер;
• на ваш при­мер.

Примеры предложений

Посмотрите на пример с составленным уравнением.
Мы смотрим на пример брата.
В новых исследованиях мы всегда опираемся на пример предшественников.
Обратим внимание на пример из статистики.
Посмотрим на пример схемы и составим похожую.
Глядя на пример, изображенный на рисунке, мы понимаем, как устроена растительная клетка.
Мы сделали вывод, сославшись на пример из проверенного источника.
Посмотрев на пример наставника, в успехе он не сомневался.

Векторная алгебра

Пример 11. Координаты вектора

Дано:
Точки: A(2, -4, 0); B(-4, 6, -2).

Найти:
Координаты вектора — ?

Решение:
Начало вектора совпадает с точкой А, конец – с точкой В. Находим координаты вектора :

Ответ:

Пример 12. Направляющие косинусы вектора

Дано:
Вектор: .

Найти:
Направляющие косинусы вектора . — ?

Решение:
Координаты вектора связаны с его направляющими косинусами следующим образом:

Ответ:

Дано:
Вектор: .

Найти:
Длину вектора . — ?

Решение:
Определяем длину вектора :

Ответ:

Пример 14. Объем параллелепипеда

Дано:
Координаты векторов:

Найти:
Объем параллелепипеда V — ?

Решение:
Объем параллелепипеда вычисляется по формуле:

Найдём смешанное произведение векторов:

Объем параллелепипеда:

Ответ: V=24.

Пример 15. Объем пирамиды

Дано:
Координаты векторов:

Найти:
Объем пирамиды V — ?

Решение:
Объем пирамиды вычисляется по формуле:

Найдём смешанное произведение векторов:

Вычисляем объём пирамиды:

Ответ: V=4.