Уравнения 2 класс по математике

Как решать показательные неравенства

Как мы уже говорили, для успешного освоения этой темы нужно хорошенько повторить все, что касается показательных уравнений. Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости…

Допустим, у нас есть простейшее показательное неравенство:

3х > 9

Если вы помните, как решались показательные уравнения, не придется долго думать, что делать с таким неравенством — приведем его к одинаковому основанию:

3х > 32

х > 2

Казалось бы, все логично, но всегда ли можно смело вычеркивать одинаковые основания степеней? А что, если вместо 3 у нас основание степени будет 0,5? Посмотрим:

0,5х > 0,52

Проверим, верно ли в таком случае х > 2.

0,52 = 0,25;

0,53 = 0, 125 и т. д.

Как видите, на самом деле в этом случае х < 2. Неудивительно, если вспомнить, о чем мы писали в самом начале, когда рисовали графики возрастающей и убывающей показательной функции.

Если а > 1, то ax > an <-> a > n, и при решении неравенства можно просто убрать одинаковые основания степени. Если 0 < а < 1, то ax > an <-> a < n, т. е. одинаковые основания по-прежнему можно убрать, но при этом необходимо поменять знак неравенства. Если a = 1, то решений нет, т. к. единица в любой степени равна сама себе.

Наконец, если рассмотреть случай, когда а < 0, получится неопределенность. Допустим:

(-3)х > 9

(-3)х > 32

Логичное, на первый взгляд, предположение, что х > 2, не выдержит проверки, потому что:

х = 3 -> (-3)3 = -27

х = 4 -> (-3)4 = 81

х = 5 -> (-3)5 = -243

Если продолжить этот ряд, знаки будут чередоваться, и наш корень будет попеременно то меньше, то больше 2. Поэтому для ясности всегда предполагается, что основание степени — положительное число.

Это были общие правила, а сейчас рассмотрим разные виды показательных неравенств и примеры с решениями.

Математика 2 класс

Итоговый тест по математике для 2 класса2 класс. Табличное умножение. Сложение и вычитание двузначных чисел. Решение задач на нахождение периметра. Решение задач на нахождение третьего слагаемого. Единицы измерения длины. Вариант №1.

1. Представь число 54 в виде суммы разрядных слагаемых     20 + 54     50 + 4     40 + 14     58 — 4

2. Сравни числа 95 и 105     95 = 105     95 < 105     95 >105

3. Разность чисел 54 и 28 равна     16     36     82     26

4. Частное чисел 48 и 6 равно     8     6     54     42

5. Произведение чисел 9 и 5 равно     14     4     45

6. Сумма чисел 56 и 17 равна     72     63     73

7. Число 28 больше 4 в     7 раз     в 24 раза     в 32 раза     в 9 раз

8. Найди другое слагаемое, если сумма двух чисел равна 48, а одно из слагаемых равно 16.     32     64     21     3

9. Значение выражения 5 • 4 + 3 • 6 равно     123     66     4     38

10. Значение выражения 40 – (26 – 3 • 5) равно     65     29     19     39

11. Число 32 больше 8     на 4     на 14     на 40     на 24

12. Сравни величины длины 4 см и 2 дм     4 см = 2 дм     4 см < 2 дм     4 см > 2 дм

13. Сравни величины длины 1м и 25 см     1 м = 25 см     1 м > 25 см     1 м < 25 см

14. Периметр (сумма длин сторон) квадрата со стороной 7 см равен     21 см     49 см     14 см     28 см

15. Витрину магазина украшают 9 кукол, а машинок в 3 раза больше. Сколько машинок украшают витрину?     12     6     27     36

16. У Зои было 100 рублей. Она купила сметану за 36 рублей, масло за 24 рубля. На остальные деньги Зоя купила колбасу. Сколько стоит колбаса?     60     40     12     80

17. Корень уравнения х : 9 = 6 равен     63     3     15     54

18. На кустике было 7 ягод клубники. 4 ягоды поспели. Сколько ягод на кустике?     11     7     0

Итоговый тест по математике 2 класс. Вариант №2.

1. Представь число 63 в виде суммы разрядных слагаемых     66 — 3     60 + 3     50 + 13     30 + 33

2. Сравни числа 99 и 101     99 = 101     99 < 101     99 >101

3. Разность чисел 54 и 9 равна     6     63     45     59

4. Частное чисел 40 и 5 равно     35     8     45     6

5. Произведение чисел 9 и 7 равно     63     16     2

6. Сумма чисел 63 и 29 равна     91     82     92

7. Число 54 больше 9     в 45 раз     в 63 раза     в 6 раз     в 9 раз

8. Найди другое слагаемое, если сумма двух чисел равна 67 а одно из слагаемых равно 15     52     82     42     4

9. Значение выражения 6 • 2 + 7 • 5 равно     23     47     545     420

10. Значение выражения 50 – (16 – 5 • 2) равно     28     14     44     50

11. Число 18 больше 3     на 6     на 15     на 21     на 11

12. Сравни величины длины 9 см и 6 дм     9 см = 6 дм     9 см < 6 дм     9 см > 6 дм

13. Сравни величины длины 3 м и 98 см     3 м = 98 см     3 м > 98 см     3 м < 98 см

14. Периметр (сумму длин сторон) квадрата со стороной 5 см равен     10 см     20 см     25 см     15 см

15. Для детского сада купили 36 мячей, а пирамидок в 4 раза меньше, чем мячей. Сколько пирамидок купили для детского сада?     40     32     9     45

16. В трех клетках было 60 кроликов. В одной клетке было 18 кроликов, в другой – 22, а остальные кролики были в третьей клетке. Сколько кроликов в третьей клетке?     40     20     18     22

17. Корень уравнения 24 : а = 8 равен     3     4     16     32

18. На столе было 12 чашек чая. 7 чашек чая гости выпили. Сколько чашек на столе?     5     12     0

Задачи по математике для 2 класса. 1. Вычисли столбиком: 53 + 37 = 86 – 35 = 33 — 7 = 36 + 23 = 80 – 56 = 58 + 5 = 65 + 17 = 88 – 81 = 85 — 9 = 2. Реши уравнения: 64 – х = 41 30 + х = 67 х — 6 = 81 3. Начерти один отрезок длиной 1 дм, а другой на 3 см короче. 4. Реши задачу: К празднику купили 17 кг груш, а яблок – на 7 кг больше. Сколько всего килограммов фруктов купили к празднику? 5. В вазе было 3 розовых и 5 красных гвоздик. После того, как поставили в вазу несколько гвоздик, их стало 25. Сколько гвоздик поставили в вазу? 6. Начертите прямоугольник со сторонами 5 см и 3 см. Найдите его периметр и площадь.

Понятие квадратного уравнения

Уравнения — это математическое равенство, в котором неизвестна одна или несколько величин. Значения неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать выражение 3 + x = 7, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Есть три вида квадратных уравнений:

• не имеют корней;
• имеют один корень;
• имеют два различных корня.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b2 − 4ac

А вот свойства дискриминанта:

• если D < 0, корней нет;
• если D = 0, есть один корень;
• если D > 0, есть два различных корня.

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

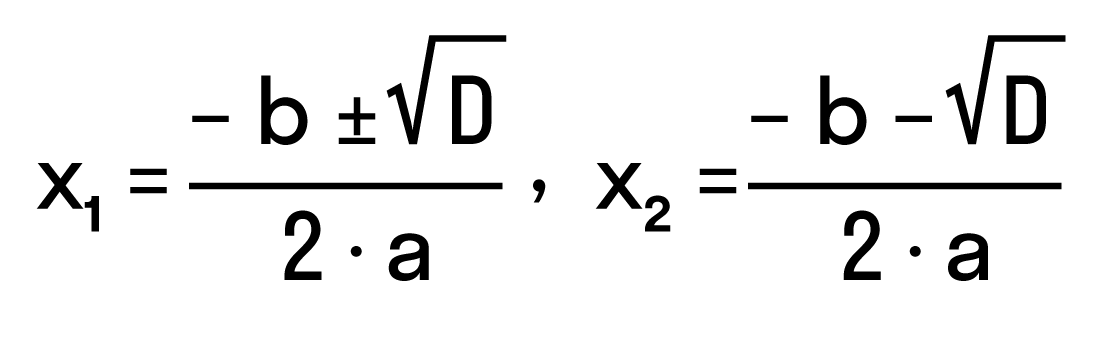
Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Выводим формулу корней квадратного уравнения

Продолжим изучать формулу корней квадратного уравнения.

Пусть перед нами есть задача решить квадратное уравнение ax2 + bx + c = 0. Выполним ряд равносильных преобразований:

• разделим обе части этого уравнения на отличное от нуля число a, после чего получим приведенное квадратное уравнение:
• выделим полный квадрат левой части нового уравнения:

  ,

  после чего уравнение примет вид

• перенесем два последних слагаемых в правую часть и сменим знак на противоположный:
• преобразуем выражение в правой части:

Так, мы пришли к уравнению , которое полностью равносильно исходному ax2 + bx + c = 0.

Отсюда выводы про корни уравнения :

И еще один вывод: есть у уравнения корень или нет, зависит от знака выражения в правой части

При этом важно помнить, что знак этого выражения задается знаком числителя. Потому выражение принято называть дискриминантом квадратного уравнения и обозначается буквой D

По значению и знаку дискриминанта можно сделать вывод, есть ли действительные корни у квадратного уравнения, и сколько.

Повторим:

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения

Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней

Алгоритм решения квадратного уравнения ax2 + bx + c = 0:

• вычислить его значение дискриминанта по формуле D = b2−4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4×2 + 28x — 49 = 0.

Как решаем:

1. Найдем дискриминант: D = 282 — 4(-4)(-49) = 784 — 784 = 0
2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
3. Найдем корень

   х = — 28/2(-4)

   х = 3,5

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6×2 = 0.

Как решаем:

1. Произведем равносильные преобразования. Умножим обе части на −1

   54 — 6×2 = 0 | *(-1)

   6×2 — 54 = 0

2. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   6×2 = 54

   х2 = 9

   х = ±√9

   х₁ = 3, х₂ = — 3

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x2— х = 0.

Как решаем:

1. Преобразуем уравнение так, чтобы появились множители

   х(х — 1) = 0

   х₁ = 0, х₂ = 1

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x2— 10 = 39.

Как решаем:

1. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   x2— 10 = 39

   x2= 39 + 10

   x2= 49

   х = ±√49

   х₁ = 7, х₂ = −7

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3×2— 4x+94 = 0.

Как решаем:

1. Найдем дискриминант по формуле

   D = (-4)2 — 4 * 3 * 94 = 16 — 1128 = −1112

2. Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Понятие уравнения

Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.

В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Определение показательного уравнения

Показательными называются уравнения с показательной функцией f(x) = aх. Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: aх = b, где a > 0, a ≠ 1.

• разложение многочлена на множители;
• свойства степенной функции;
• решение квадратных уравнений.

Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.

С точки зрения геометрии показательной функцией называют такую: y = ax, где a > 0 и a ≠ 1

У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a

Это хорошо видно на рисунке ниже.

Важно знать
Показательная функция не может быть отрицательным числом, т. е

выражение у = ax при а ≤ 0 корней не имеет.

Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.

Свойства степеней

Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.

am x an	am+n
am:an	am-n
(a x b)n	an x bn
(a : b)n	an : bn
(an)m	an x m
a-n	1/an
(a/b)-n	(b/a)n
n√a	a1/n

Как видите, ничего нового здесь нет, все это проходят в 6–7 классе.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)2- 4ac = 4n2 — 4ac = 4(n2- ac) и подставим в формулу корней:

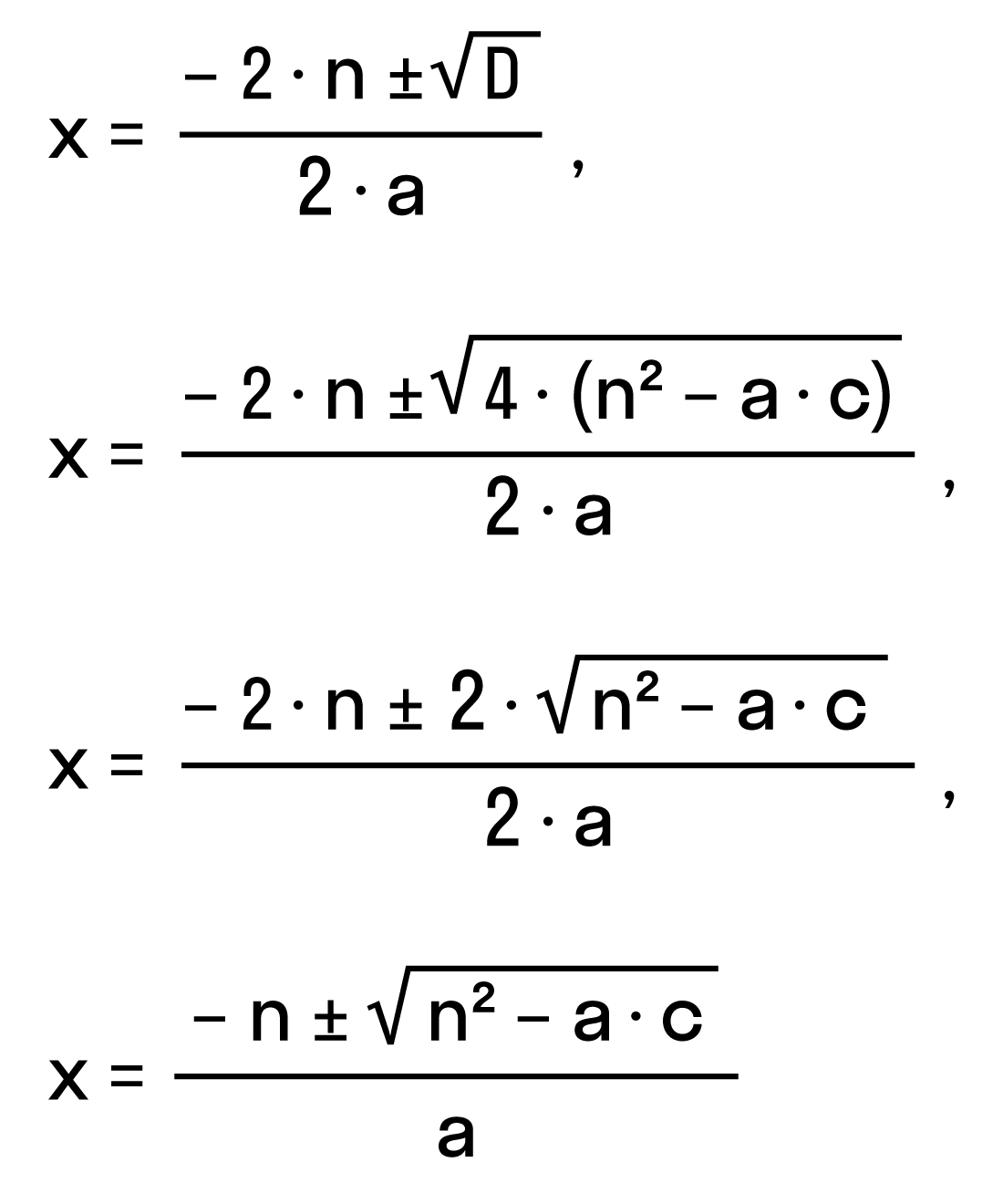
Для удобства вычислений обозначим выражение n2 -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n2- ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

• вычислить D₁= n2- ac;
• если D₁< 0, значит действительных корней нет;
• если D₁= 0, значит можно вычислить единственный корень уравнения по формуле;
• если же D₁> 0, значит можно найти два действительных корня по формуле

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11×2 — 4 x — 6 = 0, чем 1100×2 — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100×2 — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12×2- 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2×2 — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x2 + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2×2- 3x + 7 = 0 перейти к решению 2×2 + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

• x₁ + x₂ = — b/a,
• x₁* x₂ = c/a.

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3×2- 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

А еще найти корни квадратного уравнения можно с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

• Калькулятор раз
• Два
• Три

Полные и неполные квадратные уравнения

В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.

Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято назвать неполным.

Неполное квадратное уравнение —— это квадратное уравнение вида ax2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.

Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.

Для самых любопытных объясняем откуда появились такие названия:

Если b = 0, то квадратное уравнение принимает вид ax2 + 0x+c=0 и оно равносильно ax2 + c = 0. Если c = 0, то квадратное уравнение выглядит так ax2 + bx + 0 = 0, иначе его можно написать как ax2 + bx = 0. Если b = 0 и c = 0, то квадратное уравнение выглядит так ax2 = 0. Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Как решаем:

1. Перенесем 6x из левой части в правую. Знак меняем на противоположный, то есть минус.

   6x −5x = 10

2. Приведем подобные и завершим решение.

   x = 10

Ответ: x = 10.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Как решаем:

1. Сократим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.

   −4x = 12 | :(−4)
   x = −3

Ответ: x = −3.

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Алгоритм решения простого линейного уравнения
Раскрываем скобки, если они есть. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую. Приводим подобные члены в каждой части уравнения. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе.

А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = -b : а; если а равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

• кубические
• уравнение четвёртой степени
• иррациональные и рациональные
• системы линейных алгебраических уравнений

Приведенные и неприведенные квадратные уравнения

Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.

Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.

Неприведенным называют квадратное уравнение, где старший коэффициент может быть любым.

Давайте-ка на примерах — вот у нас есть два уравнения:

• x2 — 2x + 6 = 0
• x2 — x — 1/4 = 0

В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x2 ), а значит уравнение называется приведенным.

2×2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.

Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.

Запоминаем!

У преобразованного уравнения те же корни, что и у первоначального. Ну или вообще нет корней.

Пример 1. Превратим неприведенное уравнение: 8×2 + 20x — 9 = 0 — в приведенное.

Для этого разделим обе части исходного уравнения на старший коэффициент 8:

Ответ: равносильное данному приведенное уравнение x2 + 2,5x — 1,125 = 0.

Задачи на умножение и деление 2 класс в два действия

КАРТОЧКА 1

Прочитай задачи. Запиши решение и ответ.

1. В магазине продаются 5 наборов кастрюль по 3 штуки в наборе и ещё 9 кастрюль отдельно. Сколько всего кастрюль продаётся в магазине?
2. Антон поймал 16 окуней, а щук в 2 раза меньше. Сколько всего рыб поймал Антон?
3. Идёт колонна солдат: 9 рядов по 2 солдата и 3 солдата впереди. Сколько солдат идёт в колонне?

КАРТОЧКА 2

Прочитай задачи. Запиши решение и ответ.

1. Борис отжимается от пола 27 раз, а Руслан в 3 раза меньше. На сколько меньше отжиманий делает Руслан?
2. Один класс выучил 7 песен, это в 2 раза меньше, чем второй. Сколько всего песен выучили два класса?
3. Оксана сложила из спичек один шестиугольник и 8 одинаковых треугольников. Сколько спичек использовала Оксана?

КАРТОЧКА 3

Прочитай задачи. Запиши решение и ответ.

1. 12 красных и 6 жёлтых яблок разложили поровну на 2 тарелки. Сколько яблок лежит на каждой тарелке?
2. Школьники посадили 2 ряда яблонь по 8 деревьев и 17 грушевых деревьев. Сколько всего деревьев посадили школьники?
3. На трёх ветках сидело по 6 воробьёв. Прилетело ещё 13 воробьёв. Сколько стало птиц?

КАРТОЧКА 4

Прочитай задачи. Запиши решение и ответ.

1. 3 ящика с бананами весят 30 кг, а ящик с хурмой 4 кг. На сколько легче ящик с хурмой?
2. Глубина колодца 50 метров, а глубина оврага на 40 метров меньше. Во сколько раз глубина оврага меньше, чем глубина колодца?
3. Когда портниха пришила по 5 пуговиц к 3 пальто, у неё осталось 37 пуговиц. Сколько пуговиц было у портнихи?

КАРТОЧКА 5

Прочитай задачи. Запиши решение и ответ.

1. На двух этажах 14 окон. Сколько окон на трёх этажах?
2. В двух вёдрах 20 литров молока. Сколько молока в 8 таких же вёдрах?
3. Почтальон разнёс 8 журналов, а газет в 3 раза больше. Сколько газет и журналов разнёс почтальон?

КАРТОЧКА 6

Прочитай задачи. Запиши решение и ответ.

1. Таня купила 4 ручки по 3 рубля и тетрадь по 19 рублей. Сколько денег она заплатила?
2. С одной грядки собрали 17кг клубники, а с другой 13кг. Клубнику разложили в корзины по 3 кг в каждом. Сколько получилось корзин?
3. Настя собрала 38 орехов, а Петя — 42 ореха. Все орехи рассыпали в пакеты по 10 орехов в каждый. Сколько понадобилось пакетов?

КАРТОЧКА 7

Прочитай задачи. Запиши решение и ответ.

1. Для приготовления раствора строители взяли 7 кг цемента, а песка в 3 раза больше. Сколько строительного материала было приготовлено?
2. 20 яиц идёт на приготовление 10 порций омлета. Сколько яиц нужно для приготовления 5 порций?
3. У Саши 15 жёлтых шаров. Это в 3 раза больше, чем красных. На сколько меньше красных шаров у Саши?

КАРТОЧКА 8

Прочитай задачи. Запиши решение и ответ.

1. Катя нарисовала 14 картин, а её подруга в 2 раза меньше. На сколько больше картин нарисовала Катя?
2. В зале 5 колонн украсили 50 шариками. Сколько нужно шариков, чтобы украсить 8 колонн?
3. В 10 коробках — 60 карандашей. Сколько надо взять коробок, чтобы разместить 12 таких же карандашей?

КАРТОЧКА 9

Прочитай задачи. Запиши решение и ответ.

1. В трёх вазах лежало по 9 яблок. 8 яблок съели. Сколько яблок осталось?
2. Когда в кафе сидело 9 посетителей, свободных мест оставалось в 3 раза больше, сколько посетителей может принять кафе?
3. Одна курочка снесла 6 яиц, это в 3 раза меньше, чем другая. Сколько яиц они снесли вместе?

КАРТОЧКА 10

Прочитай задачи. Запиши решение и ответ.

1. Для уроков труда купили 4 набора цветной бумаги по10 листов в каждом наборе. На поделки истратили 18 листов. Сколько листов осталось?
2. Свете 18 лет, а Юля в 2 раза моложе. На сколько лет Юля младше Светы?
3. 3 утки вывели по 9 утят, а гусыня — 8. На сколько меньше родилось гусят, чем утят?

КАРТОЧКА 11

Прочитай задачи. Запиши решение и ответ.

1. Соловей летел 3 дня по 10 км и ещё день 14 км. Какой путь пролетел соловей?
2. У Алёши 63 сказки. В трёх книгах по 8 сказок, остальные на дисках. Сколько сказок на дисках?
3. Дети смастерили 54 игрушки. 10 мальчиков сделали по 2 игрушки. Сколько игрушек изготовили девочки?