Деление натуральных чисел: правила, примеры, решения

Деление методом последовательного вычитания

Только что мы говорили о делении в контексте умножения. На основе этого знания можно проводить операцию деления. Однако, существует еще один, достаточно простой и достойный внимания подход — деление методом последовательного вычитания. Этот способ понятен интуитивно, поэтому рассмотрим его на примере, не приводя теоретических выкладок.

Заголовок

Сколько будет 12 разделить на 4?

Иными словами данную задачу можно сформулировать так: имеется 12 предметов (например, апельсинов), и их нужно разделить на равные группы по 4 предмета (разложить в коробки по 4 штуки). Сколько будет таких групп или коробок по четыре апельсина в каждой?

Шаг за шагом будем отнимать от исходного количества по 4 апельсина и формировать группы по 4 до того момента, пока апельсины не закончатся. Количество шагов, которые нам придется сделать, и будет ответом на изначальный вопрос.

Из 12 апельсинов откладываем первую четверку в коробку. После этого в исходной куче апельсинов остается 12-4=8цитрусовых. Из этих восьми в другую коробку забираем еще 4. Теперь в исходной куче апельсинов осталось 8-4=4штуки. Из этих четырех штук как раз можно сформировать еще одну, отдельную третью коробку, после чего в исходной куче останется 4-4= апельсинов.

Итак, мы получили 3 коробки, по 4 предмета в каждой. Иными словами, мы разделили 12 на 4, и получили в результате 3. 

Работая с числами, не нужно каждый раз проводить аналогию с предметами. Что мы делали с делимым и делителем? Последовательно вычитали делитель из делимого, пока не получили нуль в остатке.

Важно!

При делении методом последовательного вычитания количество операций вычитания до получения нулевого остатка и есть частное от деления.

Для закрепления рассмотрим еще один, более сложный пример.

Пример 1. Деление последовательным вычитанием

Вычислим результат деления числа 108 на 27 методом последовательного вычитания.

Первое действие: 108-27=81.

Второе действие: 81-27=54.

Третье действие: 54-27=27.

Четвертое действие: 27-27=.

Более действий не требуется. Мы получили ответ:

108÷27=4

Отметим, что данный метод удобен только в случаях, когда необходимое количество последовательных вычитаний невелико. В остальных случаях целесообразно применять правила деления, которые мы рассмотрим ниже.

Как научиться делить столбиком

Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:

• Разряды натуральных чисел (десятки, сотни, тысячи). Находить их в ряду многозначных цифр.
• Таблица умножения. Этот материал лучше выучить наизусть и постоянно повторять.
• Отнимать, складывать не только однозначные или двузначные, но и многозначные числа.
• Решать маленькие задачи на умножение, разность, сумму устно.

Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:

6х2=12

6х3=18

6х4=24 и так далее.

Смело предлагайте такие примеры:

24:6=4

24:4=6

12:2=6

18:3=6

Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.

Игровые задания

Интересные математические игры на деление без остатка помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.

• Головоломки на развитие внимания. Напишите в тетради 3–5 примеров на деление с ответами.

  Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные примеры с помощью устного счета.

• Подбор примера по результату. Предлагайте малышу ответ без примера. Давайте задание придумать задачу. Например, ответ 8. Ребенок может придумать такую задачу: 48:6.
• «Идем в магазин». Расставьте на полу игрушки с карточками. На листах написаны примеры: 6:2, 18:3, 42:7, 100:50. Игрушки — это «товар» в фантазийном магазине, частное после решения примера на карточке — их цена. Чтобы узнать стоимость покупки, нужно решить задания, а потом оплатить полученный результат в кассу. Играть лучше в небольшой команде — 2–3 человека.
• «Молчуны». Ребенок получает карточки с цифрами от 1 до 100. Задавайте вопросы с примерами на деление, ученик должен отвечать без слов, показывая правильный ответ.
• Небольшие самостоятельные работы с подарком за старательность. Распечатайте карточки с примерами в количестве 5–10 штук. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей. Такой тренажёр хорошо стимулирует детей.

• «Ищем дерево».

  Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:

45:9           120:60          14:7

Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой. Получится так:

45:9=5

120:60=2

14:7=2

5+2+2=9

Ребенок должен найти дерево под номером 9.

Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.

После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком. Если педагогического опыта у вас нет и вы не знаете, как объяснить ребёнку процесс деления столбиком, то посмотрите видеоурок на эту тему, вспомните теорию сами.

Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:

1. Мама-учитель

Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал по теме “деление уголком”. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ.

Например, это:

Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.

3. Нанять репетитора

Деление (даже трёхзначных чисел на двузначные) не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом.

Этот вариант оставим на крайний случай.

Методика деления в столбик

Существует определенный алгоритм для деления в столбик. Изучается он в начальных классах средних образовательных школ. Методику можно применять не только для положительных, но и отрицательных значений. При этом нужно учитывать знак:

1. Деление отрицательной величины на отрицательную — положительное значение.
2. При делении положительного на отрицательное или наоборот — отрицательная величина.

Алгоритм без остатка

Методика применяется в том случае, когда делимое является не простым числом, а содержит множители. Кроме того, при его делении на делитель, не соответствующий одному из признаков деления. Например, 33 делится на 2 с остатком. Однако, когда делитель равен 3, то последнего нет.

Для применения алгоритма нужно наглядно разобрать следующий пример: требуется разделить 78 на 2. Методика выполнения этой операции имеет следующий вид:

1. Записать делимое с левой стороны, а делитель — справа.
2. По карточке простых чисел или при помощи ручного метода необходимо определить принадлежность делимого к простым значениям (78 делится на 2, поскольку заканчивается на четную цифру 8).
3. Разделить две значения вертикальной чертой.
4. Выделить I неполное делимое: 7.
5. По таблице умножения подобрать ближайшее целое (3). При произведении его на делитель должно получиться значение, которое меньше первого неполного делимого (3 * 2 = 6 < 7). Если записать 4, то 4 * 2 = 8 > 7 (вариант не подходит).
6. Записать число, полученное при умножении делителя на подобранное значение, под I неполным делимым. Произвести операцию вычитания (7 — 6 = 1).
7. Результат вычитания (1), который называется остатком, не делится на 2. Следовательно, нужно дописать II неполное делимое (18). Если по какой-то причине, результат делится на делитель, то подобранное значение является неверным.
8. Значение 18 делится на 2, т. е. 18/2 = 9.
9. Результат деления 78 на 2 равен 39.

Операция с остатком

Не во всех случаях результат деления двух чисел является целой величиной. В школьной программе встречается группа примеров, в которых требуется найти остаток, полученный при выполнении операции деления 2 значений (77/3). Алгоритм похож на предыдущий, но имеются некоторые особенности:

1. Два числа записываются, как и в предыдущем случае.
2. Принадлежность к множеству простых чисел не проверяется.
3. Выделить I неполное делимое: 7.
4. Подобрать ближайшее целое число, записав его в результат: 2.
5. Выполнить проверку: 3 * 2 = 6 < 7 (значение подходит).
6. Записать 6 под 7, а затем выполнить операцию вычитания: 7 — 6 = 1. Остаток меньше 3, следовательно, число подобрано правильно.
7. Выполнить подбор множителя для 17: целочисленного значения нет. Следовательно, нужно подобрать ближайшее целое: 5.
8. Произвести проверку: 3 * 5 = 15 < 17.
9. Записать 5 в результат и определить остаток: 17 — 15 = 2.
10. Результат деления 77 на 3 эквивалентен: 25 с остатком 2.

Таким образом, для выполнения операции деления двузначного числа на однозначное нужно знать признаки делимости величин, а также основные алгоритмы деления с остатком и без него.

Как научить ребенка делению – закрепляем навык

Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.

1. «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
2. «Деление. Уровень 4. Рабочая тетрадь» от Kumon
3. «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина – автора обучающих книг-бестселлеров

Самым главным, когда вы учите ребёнка делению в столбик, является  усвоение алгоритма, который, в общем-то, достаточно прост.

Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей

Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода

Для того чтобы легко научить ребёнка операции деления нужно:

• Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
• Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.

Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.

Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.

Деление произведения на число

Произведение можно разделить на число двумя способами:

1) Чтобы разделить произведение на какое-нибудь число, можно сначала вычислить значение произведения (выполнить умножение) и полученный результат разделить.

Например, чтобы найти значение выражения:

(12 · 5) : 3,

можно сначала умножить  12  на  5:

12 · 5 = 60

и полученное произведение разделить на  3:

60 : 3 = 20,

значит  (12 · 5) : 3 = 60 : 3 = 20.

Если один из сомножителей делится на число, на которое надо разделить произведение, то можно воспользоваться вторым способом нахождения частного от деления произведения на число.

2) Чтобы разделить произведение на какое-нибудь число, можно разделить на это число один любой сомножитель, оставив другие без изменений.

Например, чтобы найти значение выражения:

(8 · 20) : 4,

можно сначала разделить любой из сомножителей  (8  или  20)  на  4:

8 : 4 = 2

и полученное частное умножить на другой сомножитель:

2 · 20 = 40,

значит  (8 · 20) : 4 = (8 : 4) · 20 = 2 · 20 = 40.

Данное выражение можно решить ещё так:

(8 · 20) : 4 = 8 · (20 : 4) = 8 · 5 = 40.

Деление целых положительных чисел

Целыми положительными числами называют натуральные числа, поэтому деление целых положительных чисел производится, исходя из правил деления натуральных чисел. Рассмотрим несколько примеров для детального просмотра деления целых положительных чисел.

Пример 1

Произвести деление целого положительного 104 на целое положительное 8.

Решение

Для упрощения процесса деления можно представить число 104 в виде суммы 80+24,теперь необходимо применить правило деления суммы на данное число. Получим 1048=(80+24)8=808+248=10+3=13.

Ответ: 1048=13.

Пример 2

Найти частное от деления 308 716452.

Решение

Когда имеем большое число, деление лучше всего производить в столбик:

Ответ: 308 716452=683.

Как объяснить деление столбиком

Сначала стоит доходчиво объяснить, что такое деление на простом примере. Суть математического действия — разложить число поровну. В 3-м классе дети хорошо учатся на доступных примерах: раздают кусочки торта гостям, рассаживают кукол по 2 машинам.

Когда малыш усвоит суть деления, покажите его запись на листке. Используйте уже знакомые задания с простыми числами:

• Сначала запишите задачу обычным способом: 250:2=?
• Каждому числу дайте название: 250 — делимое, 2 — делитель, результат после знака равно — частное.
• Затем сделайте сокращенную запись столбиком (уголком):

• Рассуждайте вместе так: сначала найдем неполное частное. Для этого нам потребуется сравнивать первое неполное делимое и делитель. Это будет 2, так как оно не меньше делителя, а вернее, равно ему. В этом числе помещается один делитель, значит, в частное записываем цифру 1 и умножаем ее на 2. Заносим полученный результат под делимым. Отнимаем 2-2. Получится ноль, поэтому сносим следующее число и опять подыскиваем частное. Совершаем математическое действие до тех пор, пока не получится ноль.
• После получения окончательного результат сделайте проверку с помощью умножения: 125х2=250.

Во время объяснения правил деления в столбик желательно научить третьеклассника рассуждать в процессе вычисления вслух, выполнять действия на черновике.

Сначала проговаривайте алгоритм вместе, потом только слушайте ученика и помогайте исправить ошибки.

На заметку! Приучайте малыша постоянно проверять себя. Школьник должен понимать, что величина остатка вычитания в столбике деления должен всегда быть меньше делителя.

Примеры деления числа на произведение

Пример 1. Применить правило деления числа на произведение двух чисел:
24 : ( 3 * 4).

Как рассуждаем:

1. Чтобы разделить число на произведение, вычислим сначала произведение в скобках: 3 * 4 = 12.
2. Подставляем полученное число в выражение:

24 : ( 3 * 4) = 21 : 12 = 2.

Вот и ответ. А теперь решим это же выражение другим способом.

1. Чтобы разделить число на произведение чисел, нужно сначала число 24 разделить на первый множитель 3. А после, разделить полученный на второй множитель 8:

24 : ( 3 * 4) = 24 : 3 : 4 = 8 : 4 = 2.

А как можно еще решить это выражение?

1. Чтобы число разделить на произведение, нужно сначала число 24 разделить на второй множитель 4. И полученный результат разделить на первый множитель 3:

24 : ( 3 * 4) = 24 : 4 : 3 = 6 : 3 = 2.

Вот, как это работает! Мы нашли значение выражения разными способами, при этом результаты получились одинаковыми.

Пример 2. Вычислить: тысячу разделить на произведение двадцати и пяти.

Ответ:

1000 : (20 * 5) = 1000 : 100 = 100

1000 : (20 * 5) = 1000 : 20 : 5 = 500 : 5 = 10

1000 : (20 * 5) = 1000 : 5 : 2 = 200 : 2 = 10

Деление на единицу с любым количеством нулей

При делении на единицу натуральное число, над которым проводится операция деления, не будет меняться, так как деление на единицу в результате дает делимое. По сути, число делится лишь один раз: полностью и без остатков.

При делении на единицу с любым количеством нулей данное количество должно учитываться в результате. Так как число остается в таком же виде, нули уходят вперед или отбрасываются.

Если делимое содержит нули, то количество нулей делимого отбрасывается ровно на столько, сколько нулей в делителе.

Данное действие приведет к появлению десятичной дроби, то есть дроби, где сначала записывается нуль, потом запятая, а после некоторое количество нулей и разделенное число.

Деление с остатком и неполное частное

Но не всегда можно одно число разделить на другое. Вернее сказать, что не всегда можно сделать это полностью. Например, 37 нельзя разделить на 5, потому что нет такого натурального числа, умножив которое на 5, мы получили бы 37. В этом случае говорят, что 37 не делится нацело на 5.

К примеру, если мы захотим раздать все 37 яблок поровну между пятью детьми, то у нас это сделать не получится. Мы сможем раздать (использовать из всего количества яблок) только по 7 яблок каждому ( \(\textcolor{red} {7\cdot 5=35}\) ), и у нас останется 2 яблока ( \(\textcolor{red} {37-35=2}\) ).

В таком случае действие деление также состоит из делимого (в нашем случае 37) и делителя (5). Полученное число 7 называется неполное частное, потому что не все делимое число мы смогли разделить на необходимое число частей. А разница между полным делимым (37) и использованными из него единицами (35), то есть число 2, называется остаток.

Итак, деление с остатком – это нахождение
такого наибольшего целого числа, умножив которое на делитель, мы получим число,
максимально близкое к делимому, но не превосходящее его. Это искомое число
называется неполное частное. Разница
между делимым и неполным частным называется остаток.

Остаток всегда меньше делителя!

Отсюда следует общий вид действия деления натуральных чисел для случаев деления без остатка и с остатком.Разделить целое число a (делимое) на целое число b (делитель) означает найти такие числа c и d, при которых справедливы следующие соотношения: \(\textcolor{red} {a=b\cdot c+d}\) ; \(\textcolor{red} {d<b}\) .Если \(\textcolor{red} {d=0}\) , тогда говорят, что a делится на b без остатка.

Компоненты действия
деление с остатком:

Способ 5: деление столбца на ячейку

Но, что делать, если нужно разделить столбец на содержимое одной ячейки. Ведь по принципу относительности ссылок координаты делимого и делителя будут смещаться. Нам же нужно сделать адрес ячейки с делителем фиксированным.

1. Устанавливаем курсор в самую верхнюю ячейку столбца для вывода результата. Ставим знак «=». Кликаем по месту размещения делимого, в которой находится переменное значение. Ставим слеш (/). Кликаем по ячейке, в которой размещен постоянный делитель.

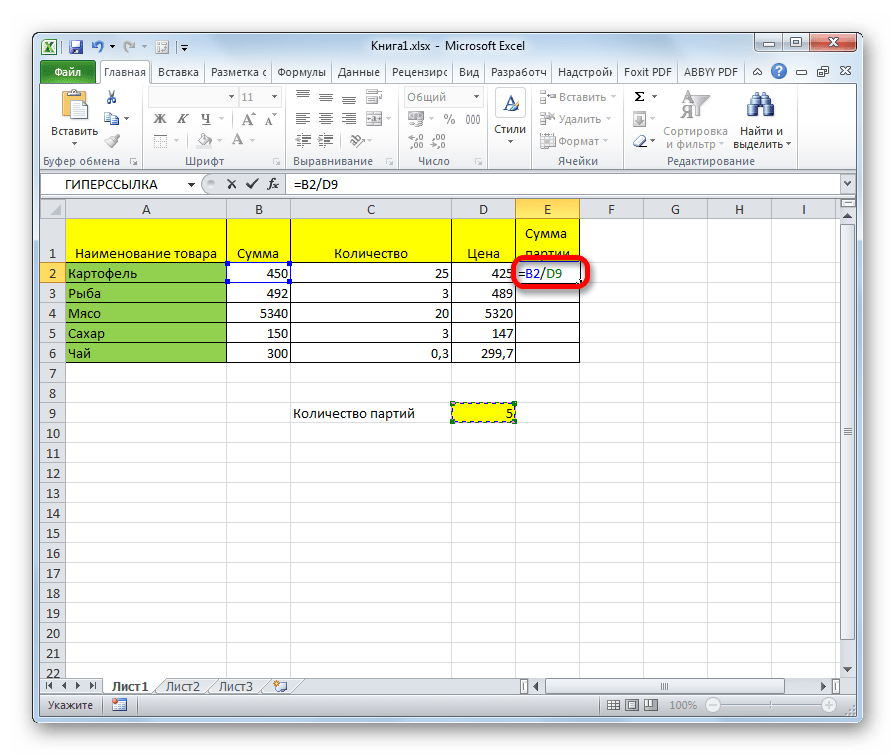
Для того, чтобы сделать ссылку на делитель абсолютной, то есть постоянной, ставим знак доллара ($) в формуле перед координатами данной ячейки по вертикали и по горизонтали. Теперь этот адрес останется при копировании маркером заполнения неизменным.

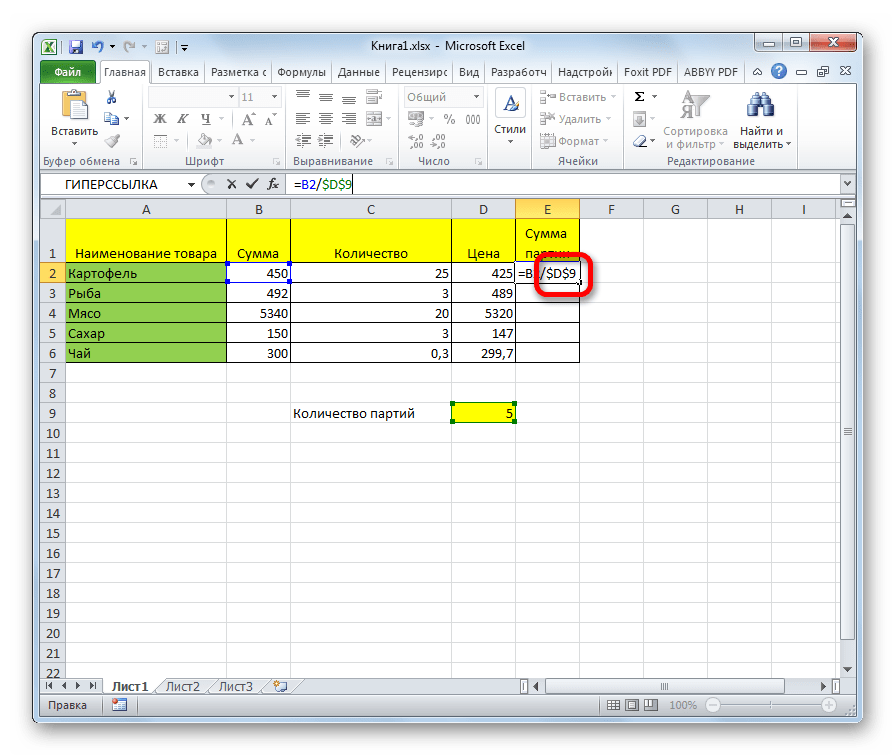
Жмем на кнопку Enter, чтобы вывести результаты расчета по первой строке на экран.

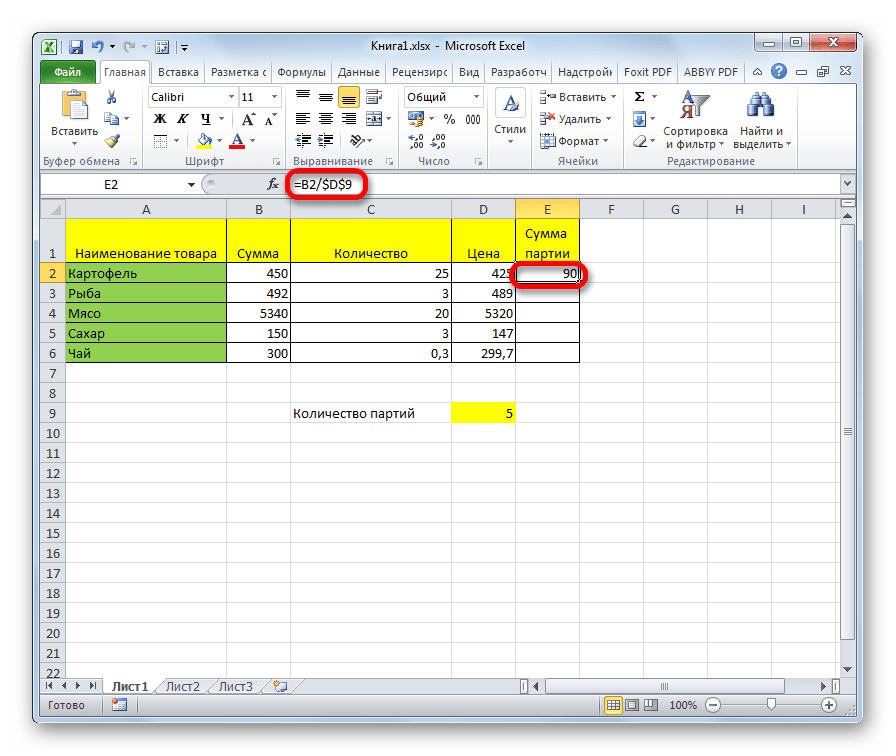
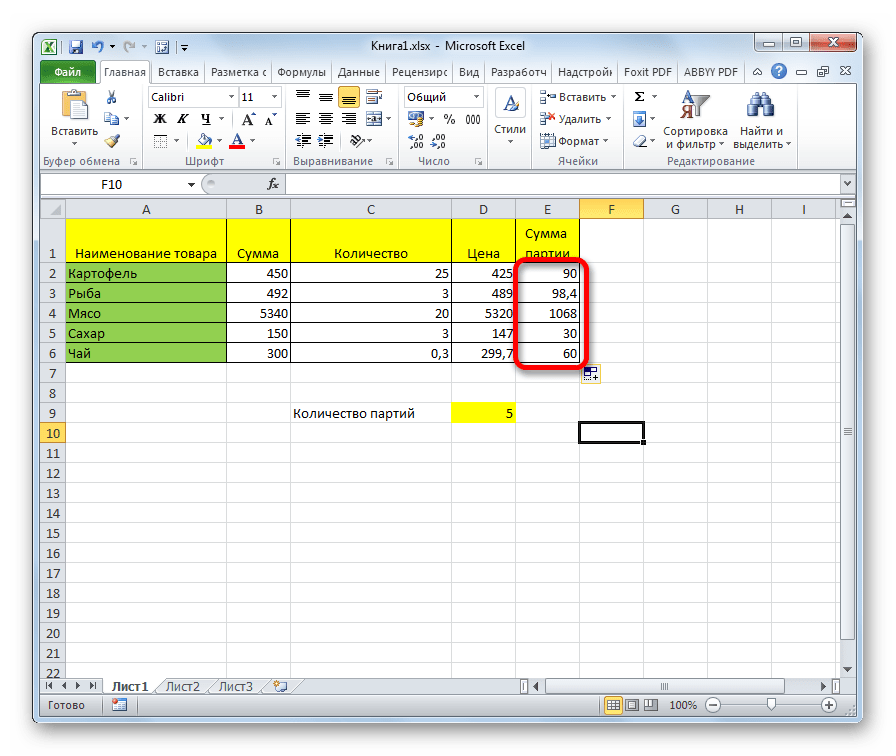
С помощью маркера заполнения копируем формулу в остальные ячейки столбца с общим результатом.

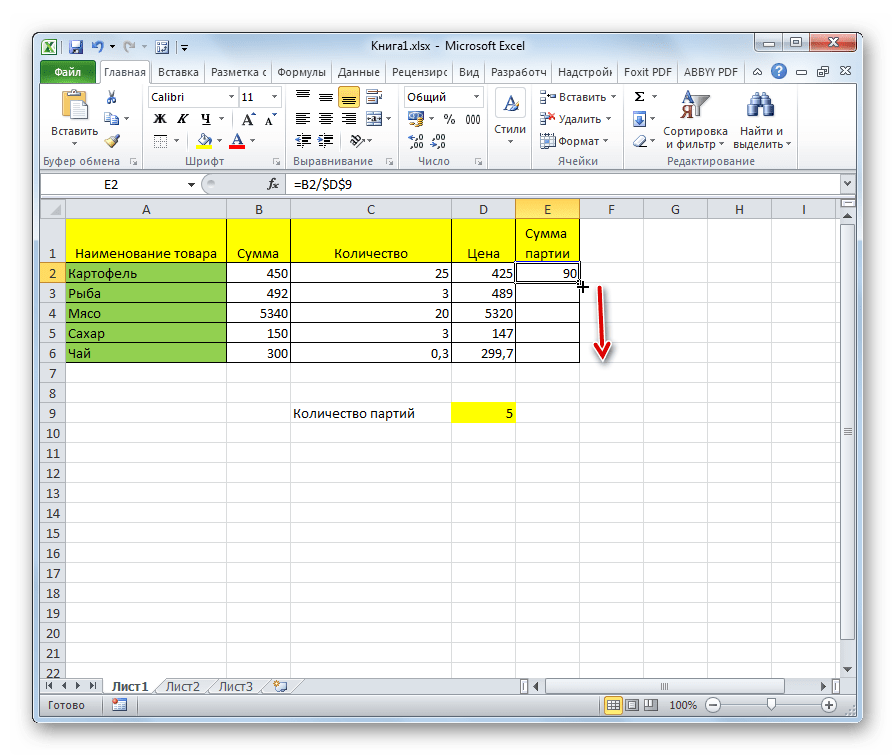
После этого результат по всему столбцу готов. Как видим, в данном случае произошло деление колонки на ячейку с фиксированным адресом.

Урок: Абсолютные и относительные ссылки в Excel

Как распределить текст с разделителями на множество столбцов.

Изучив представленные выше примеры, у многих из вас, думаю, возник вопрос: «А что, если у меня не 3 слова, а больше? Если нужно разбить текст в ячейке на 5 столбцов?»

Если действовать методами, описанными выше, то формулы будут просто мега-сложными. Вероятность ошибки при их использовании очень велика. Поэтому мы применим другой метод.

Имеем список наименований одежды с различными признаками, перечисленными через дефис. Как видите, таких признаков у нас может быть от 2 до 6. Делим текст в наших ячейках на 6 столбцов так, чтобы лишние столбцы в отдельных строках просто остались пустыми.

Для первого слова (наименования одежды) используем:

Как видите, это ничем не отличается от того, что мы рассматривали ранее. Ищем позицию первого дефиса и отделяем нужное количество символов.

Для второго столбца и далее понадобится более сложное выражение:

Замысел здесь состоит в том, что при помощи функции ПОДСТАВИТЬ мы удаляем из исходного содержимого наименование, которое уже ранее извлекли (то есть, «Юбка»). Вместо него подставляем пустое значение «» и в результате имеем «Синий-M-39-42-50». В нём мы снова ищем позицию первого дефиса, как это делали ранее. И при помощи ЛЕВСИМВ вновь выделяем первое слово (то есть, «Синий»).

А далее можно просто «протянуть» формулу из C2 по строке, то есть скопировать ее в остальные ячейки. В результате в D2 получим

Обратите внимание, жирным шрифтом выделены произошедшие при копировании изменения. То есть, теперь из исходного текста мы удаляем все, что было уже ранее найдено и извлечено – содержимое B2 и C2

И вновь в получившейся фразе берём первое слово — до дефиса.

Если же брать больше нечего, то функция ЕСЛИОШИБКА обработает это событие и вставит в виде результата пустое значение «».

Скопируйте формулы по строкам и столбцам, на сколько это необходимо. Результат вы видите на скриншоте.

Таким способом можно разделить текст в ячейке на сколько угодно столбцов. Главное, чтобы использовались одинаковые разделители.

Как делить столбиком

Допустим, нам нужно разделить  780  на  12,  записываем действие в столбик и приступаем к делению:

Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:

это число  7,  так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число  78  больше делителя, поэтому мы начинаем деление с него:

В нашем случае число  78  будет неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.

Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра —  0,  это значит, что частное будет состоять из  2  цифр.

Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:

Приступаем к делению. Нам нужно определить сколько раз  12  содержится в числе  78.  Для этого мы последовательно умножаем делитель на натуральные числа  1, 2, 3, …,  пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число  6,  записываем его под делитель, а из  78  (по правилам вычитания столбиком) вычитаем  72  (12 · 6 = 72).  После того, как мы вычли  72  из  78,  получился остаток  6:

Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше

К получившемуся остатку —  6,  сносим следующую цифру делимого —  0.  В результате, получилось неполное делимое —  60.  Определяем, сколько раз  12  содержится в числе  60.  Получаем число  5,  записываем его в частное после цифры  6,  а из  60  вычитаем  60  (12 · 5 = 60).  В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит  780  разделилось на  12  нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:

780 : 12 = 65.

Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить  9027  на  9.

Определяем неполное делимое — это число  9.  Записываем в частное  1  и из  9  вычитаем  9.  В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:

Сносим следующую цифру делимого —  0.  Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль  (0 : 9 = 0)  и в промежуточных вычислениях из  0  вычитаем  0.  Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:

Сносим следующую цифру делимого —  2.  В промежуточных вычислениях вышло так, что неполное делимое  (2)  меньше, чем делитель  (9).  В этом случае в частное записывают нуль и сносят следующую цифру делимого:

Определяем, сколько раз  9  содержится в числе  27.  Получаем число  3,  записываем его в частное, а из  27  вычитаем  27.  В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит число  9027  разделилось на  9  нацело:

9027 : 9 = 1003.

Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить  3000  на  6.

Определяем неполное делимое — это число  30.  Записываем в частное  5  и из  30  вычитаем  30.  В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:

Сносим следующую цифру делимого —  0.  Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из  0  вычитаем  0:

Сносим следующую цифру делимого —  0.  Записываем в частное ещё один нуль и в промежуточных вычислениях из  0  вычитаем  0.  Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток —  0.  Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:

Так как в делимом больше не осталось цифр, значит  3000  разделилось на  6  нацело:

3000 : 6 = 500.