Математика: деление и умножение в столбик

Правило умножения чисел столбиком

Чтобы умножить два числа столбиком, нужно два числа поместить друг над другом, правая, крайняя цифра нижнего числа, должна находиться под крайней правой цифрой верхнего числа.

Слева от двух чисел ставится знак умножения.

Под двумя цифрами чертится горизонтальная линия.

Берется второе число и первая цифра справа(5) и умножается на верхнее число(34), 5 * 34 = 170

Результат умножения записывается так, чтобы крайняя цифра результата находилась под цифрой, на которую умножали. (0 под 5.)

Если у второго числа есть следующая цифра по счету, начиная справа, то берется она (2) и умножается верхнее число на эту цифру (34 * 2 = 68). Таким образом перемножаем все цифры второго числа на верхнее!

Результат сносится за черту, опять, чтобы крайняя правая цифра результата, находилась в столбик аод цифрой на которую умножали( 8 под 2.)

И далее складываем каждый столбик и заносим результат под вторую горизонтальную линию.

Умножить столбиком двузначное на двузначное число.

Для того, чтобы умножить “двузначное на двузначное число столбиком” – 36 на 98, выравниваем два числа по правому краю.

Разбиваем наши умножаемые два числа на два простых умножения 36 на 8, и 36 на 9 – умножаем, как уже было рассказано

№2 на скрине ниже – 36 * 8 = 288.

Берем полученный результат и заносим в умножение №1, чтобы крайняя цифра результата, оказалась под числом, на которое умножали. Под цифрой 8 цифра 8 – выделено красным.

№3 на скрине ниже – 36 * 9 = 324.

Опять берем полученный результат и и заносим в умножение №1, ставим таким образом, чтобы крайняя цифра результат оказалась под цифрой, на которую умножали. 4 под 9 – выделено зеленым.

Далее складываем столбцы: крайнюю 8 синоним под вторую черту без изменений.

Второй столбец справа 4 + 8 = 12, 2 сносим под черту, один в уме.

Третий столбец справа 2 + 2 = 4 и прибавляем 1, который в уме = 5 – сносим под черту.

Четвертый столбец справа, 3 сносим без изменений.

Основные понятия

Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.

Название числа напрямую зависит от количества знаков. Однозначное — состоит из одного знака. Двузначное — из двух. Трехзначное — из трех и так далее.

Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.

• Разряд единиц — то, чем заканчивается любое число.
• Разряд десятков — то, что находится перед разрядом единиц.
• Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.

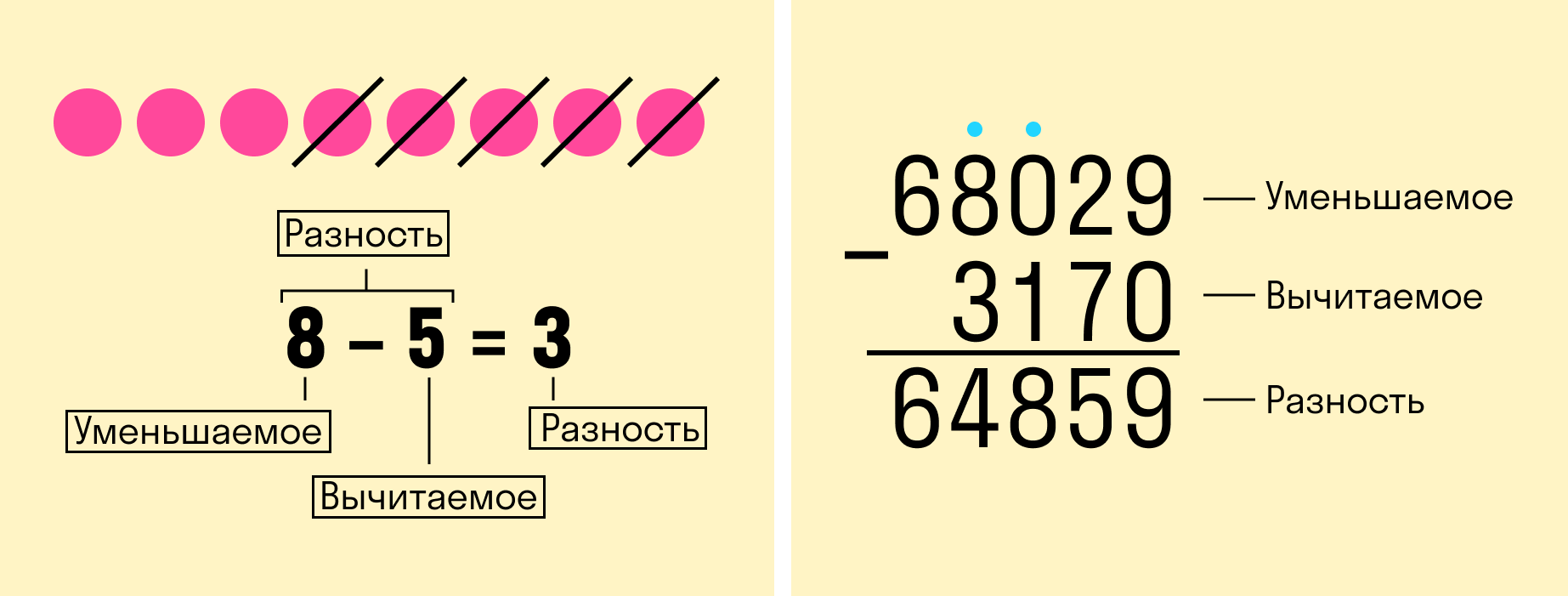
Вычитание — это арифметическое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее — вычитаемым. Результат их вычитания — разностью.

Вычитание нуля из числа не изменяет этого числа. a — 0 = a Если из числа вычесть само это число, то разность равна нулю. a — a = 0 Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое. a — (b + c) = a — b — c Чтобы вычесть число из суммы, можно вычесть это число из одного слагаемого и полученную разность прибавить к сумме остальных слагаемых. (a + b) — c = (a — c) + b = a + (b — c) Чтобы прибавить разность к числу, можно прибавить к нему уменьшаемое и из полученной суммы вычесть вычитаемое. а + (b — c) = a + b — c

Алгоритм вычитания в столбик

Вычитать столбиком проще, чем считать в уме, особенно при действиях с большими числами. Этот способ наглядный — помогает держать во внимании каждый шаг.

Рассмотрим алгоритм вычитания в столбик на примере: 4312 — 901.

Шаг 1. При вычитании столбиком самое главное — правильно записать исходные данные, чтобы самая правая цифра первого числа была под правой цифрой второго числа.

Большее число (уменьшаемое) записываем сверху. Слева между числами ставим знак минус. Вот так:

Шаг 2. Вычитание столбиком начинаем с самой правой цифры. Вычитаем по цифре (знаку). Результат записываем под чертой.

Шаг 3. Далее вычитаем из второй цифры справа: из «1» ноль.

Шаг 4. Теперь нам нужно вычесть из «3» девять. Это сделать невозможно. Поэтому займем десятку у соседа слева от тройки. Это цифра «4». Поставим над четверкой точку. Занятый десяток прибавим к «3»: 10 + 3 = 13.

Из «13» вычтем девять: 13 − 9 = 4.

Так как мы заняли десяток у «4», значит четверка уменьшилось на единицу. Об этом нам напоминает точка над «4»: 4 − 1 = 3. Вот, как это выглядит:

Рассмотрим пример вычитания в столбик чисел с нулями: 1009 — 423.

Шаг 1. Запишем числа в столбик. Большее число ставим сверху.

Вычитаем справа налево по одной цифре.

Шаг 2. Так как из нуля нельзя вычесть «2», занимаем у соседней цифры слева (ноль). Поставим над «0» точку. У нуля занять нельзя, поэтому смотрим на следующую цифру. Занимаем у «1» и ставим над ней точку. Теперь вычитаем не из нуля двойку, а из «10». Вот так:

Запоминаем!
Если при вычитании столбиком над нулем стоит точка, значит ноль превращается в «9».

Шаг 3. Над нулем стоит точка, поэтому нуль превращается в «9». Вычитаем из «9» четыре: 9 − 4 = 5.

Над «1» стоит точка. Единица уменьшается на «1»: 1 − 1 = 0. Если в результате разности левее всех цифр стоит ноль, то его записывать не надо.

Изменение частного при изменении делимого и делителя

При рассмотрении
изменений частного в результате изменений делимого и делителя предполагается,
что действие деление происходит без остатка. В противном случае изменения могут
быть не такими, о которых идет речь ниже.

При увеличении делимого в определенное количество раз, частное увеличится в это же количество раз, а при уменьшении – уменьшится.

Если мы в примере \(\textcolor{red} {24\div 4=6}\) делимое увеличим, к примеру, в 3 раза, то мы можем переписать это выражение в виде \(\textcolor{red} {(24+24+24)\div 4}\). Используя свойство деления суммы на число, мы увидим, что теперь нам нужно сложить три слагаемых, каждое из которых равно начальному выражению: \(\textcolor{red} {24\div 4+24\div 4+24\div4}\). Отсюда очевидно, что результат будет больше начального в 3 раза.

Если мы в этом же примере \(\textcolor{red} {24\div 6}\) уменьшим делимое в 3 раза, то есть, разделим его на три равные части, то очевидно, что результат деления одной части на 6 будет в 3 раза меньше, чем результат деления трех таких же частей. Посмотрите сами. Начальное выражение \(\textcolor{red} {24\div 6}\) можно записать в виде: \(\textcolor{red} {(8+8+8)\div 6=8\div 6+8\div 6+8\div 6}\), а уменьшенное в 3 раза делимое даст нам только одно из трех таких слагаемых: \(\textcolor{red} {8\div 6}\).

При увеличении делителя в определенное количество раз, частное уменьшится в это же количество раз, а при уменьшении – увеличится.

Действительно, изменение
делителя означает, что делимое необходимо разделить на большее или меньшее
количество равных частей. Соответственно, если нужно разделить на большее число
частей, то каждая часть будет меньше, чем изначально, а если делить на меньшее
число частей, то каждая часть будет крупнее.

В случае одновременного изменения делимого и делителя, частное может вести себя по-разному, или же вообще оставаться без изменений. Если нужно узнать, станет оно больше или меньше, нужно сперва посмотреть, как частное изменится после изменения делимого, а потом – как изменится после изменения делителя.

При увеличении или уменьшении делимого и делителя в одинаковое количество раз, частное не меняется.

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
—	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x2	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
1/x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»

Проверка деления

Так как делимое – это
делитель, умноженный на частное и плюс остаток, что следует из определения
деления, то результат выполнения деления можно проверить умножением.

Например:

После того, как мы умножили частное 241 на делитель 33, а к полученному произведению прибавили остаток 9, мы получили число 7962, что равно делимому. Значит, можно с большой уверенностью сказать, что действие деление выполнено верно.

Если в результате
действия деления не получилось остатка, то деление можно проверить и делением.
Действительно, если делимое – это произведение делителя и частного, то разделив
делимое на частное (один из сомножителей), мы должны получить второй
сомножитель, то есть, делитель.

 Например:

Обучение делению в столбик в тетради

Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.

Пример деления

Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.

Объяснять математическое действие нужно подробно:

• Напишите в тетради пример: 105 разделить на 5.
• Запишите это, как при делении в столбик.
• Расскажите, что 105 – делимое, а 5 – делитель.
• С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
• В столбике деления, под числом 5, напишите цифру 2.
• Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
• Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
• В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.

Родителям нужно объяснить, что это деление не имеет остатка.

Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66, а после к 232, 342, 345, и так далее.

Еще один пример деления

Как объяснить ребенку, что такое умножение и деление

Причина непонимания умножения и деления в большинстве случаев кроется в банальном отсутствии внимательности у школьника

В раннем возрасте деткам сложно концентрировать внимание на чем-то конкретном более 15 минут, поэтому они поддаются влиянию различных отвлекающих факторов

Обратите внимание! Ребенок может стесняться задавать учителю один и тот же вопрос несколько раз, потому что боится показаться глупым в глазах окружающих. В такой ситуации нужно провести со школьником беседу, уточнить детали, которые ему непонятны после объяснения материала, и успокоить

Для того чтобы объяснить ребенку понятие «умножение», для начала нужно подготовить распечатку таблицы умножения Пифагора (нарисовать ее собственноручно или распечатать на принтере). Без такой таблицы не получится разъяснить сам принцип только с помощью обычных примеров. На начальном этапе пусть ребенок сам постарается определить закономерность (желательно, чтобы это занятие стало увлекательной игрой).

Изучая данный раздел математики, детишкам должны быть известны такие простые действия, как сложение и вычитание. Разъясняя своему чаду принцип работы умножения, рекомендуется использовать самый элементарный прием. Нужно разобраться, что фраза «умножить число шесть на число два» или же «шестью два» означает то же самое, что и «шесть плюс шесть». Также следует записать пример в виде цифр для визуализации: 6*2 = 6+6.

Таблица умножения Пифагора

Объяснение принципа деления

Для того чтобы разъяснить ребенку, как нужно правильно делить, совсем необязательно использовать скучные учебники. Вместо них можно взять яблоки, конфеты и игрушки. Взрослый должен попросить карапуза разделить между тремя – четырьмя куклами пять конфеток или яблок, а далее количество фруктов следует постепенно увеличивать до 8-10.

Важно! Малыш сначала будет раскладывать предметы медленно, делая большие паузы, но кричать на него категорически запрещено, лучше запастись терпением. После того, как сладости или фрукты были разделены между игрушками, пусть ребенок посчитает, сколько их получилось у каждой куклы и поведет итог

Если было 6 карамелек и их раздали трем куклам – каждой досталось по 2. После чего родитель должен объяснить своему ребенку, что «разделять» означает «раздать всем поровну»

После того, как сладости или фрукты были разделены между игрушками, пусть ребенок посчитает, сколько их получилось у каждой куклы и поведет итог. Если было 6 карамелек и их раздали трем куклам – каждой досталось по 2. После чего родитель должен объяснить своему ребенку, что «разделять» означает «раздать всем поровну».

Еще один игровой пример представлен делением на цифрах. Нужно сказать карапузу, что цифры – это те же фрукты или конфеты и приучать, что количество сладостей, которые следует разделить, принято называть «делимое». А люди, на которых делятся конфеты, – это «делитель».

Как делать проверку

Проверка деления производится с помощью умножения: делитель умножается на делитель. Делать это можно столбиком:

Теперь проверим:

Для проверки деления с остатком нужно:

1. Умножить полное частное на делитель.
2. Прибавить к результату остаток.

17х2=34

34+1 (остаток) =35

Алгоритм проверки правильности решения примера деления не изменяется от разрядности цифр.

Видео: как научиться делить в столбик

Обучение делению столбиком десятичных дробей с запятой

Деление десятичных дробей

Чтобы ребенок сориентировался в этом математическом действие, ему необходимо разложить информацию «по полочкам»:

Десятичная дробь допускает деление не только на десятичную дробь, но и на целое значение. В таких задачах необходимо действовать, как с обычными примерами. Только когда у делимого закончатся значения до запятой, ее нужно поставить в частное. Далее деление тоже протекает привычным способом.

Десятичные дроби так же делятся на десятичные дроби. В этом математическом действии нужно убрать запятые у второго числа. Для этого требуется перенести ее вправо в обоих значениях на то количество цифр, которое отделено у делителя.

Решение задач на движение в противоположных направлениях

Мы с вами на предыдущем уроке уже познакомились с величинами, которые встречаются в задачах на движение. Давайте вспомним ключевые формулы!

Сегодня нам  встретится  новое понятие «скорость удаления». Что это такое?

Например, от автобусной остановки отъехали в разных направлениях Дима на велосипеде и Валера на мотоцикле. Скорость Димы – 10 км/ч,  а Валеры –  50 км/ч. Скорость удаления 10 + 50 = 60 км/ч.

Решим вместе задачу.

Задача

Улитки Бэлла и Элла ползли по одной дорожке в разных направлениях. Одна – на юг, другая – на север. Скорость движения Бэллы – 5 м/мин, а скорость движения Эллы – 7 м/мин. Через сколько минут расстояние между улитками будет 120 м?

Найдем скорость удаления двух улиток.

5 + 7 = 12 (м/мин)

Найдем время, зная расстояние 120 м и скорость 12 м/мин.

t= S v

120 : 12 = 10 (мин)

Ответ: 10 минут

Решение можно записать выражением 120 : (5 + 7) = 10

Решим задачу, обратную данной. Пусть время 10 минут будет известно, расстояние, которое преодолели улитки – 120 м. Скорость Бэллы – 5 м/мин. А вот скорость Эллы нам нужно найти.

Зная расстояние и время, найдем скорость удаления улиток.

v = St

120 : 10 = 12 (м/мин)

Найдем скорость Эллы.

12 – 5 = 7 (м/мин)

Ответ: 7 м/мин

Решение задачи можно записать в виде выражения (120 : 10) – 5 = 7

Следующую задачу решите самостоятельно. Внимательно рассмотрите схематический рисунок.

Красный и зеленый автомобили выехали в противоположных направлениях. Скорость красного автомобиля – 60 км/м, а зеленого – 40 км/м. Через некоторое время расстояние между красной и зеленой машинами стало 500 км. Найди это время.

Проверь себя.

60 + 40 = 100 (км/ч) – скорость удаления красной и зеленой машин.

500 : 100 = 5 (ч) – будут в пути.

Ответ: 5 часов.

Решение можно записать в виде выражения 500 : (60 + 40) = 5

Сегодня на уроке мы научились умножать и делить на числа, оканчивающиеся нулями, познакомились с правилом деления с остатком, узнали новое понятие «скорость удаления».

Алгоритм деления столбиком

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : , 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

В соответствии с алгоритмом имеем:

4·=<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.

Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.

3. Столбиком вычитаем  из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем. 

4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — . В итоге отмечаем новое рабочее число — 20.

Важно!

Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на , 1, 2, 3..  получаем:

4·5=20

Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение. 

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=.

4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.

Принимаем это число за рабочее и снова выполняем пункты  алгоритма.

2. Умножаем делитель на , 1, 2, 3.. и сравниваем результат с отмеченным числом.

4·=<2; 4·1=4>2

Соответственно, под отмеченным числом записываем число , и под делителем в следующий разряд частного также записываем .

3. Выполняем операцию вычитания  и под чертой записываем результат.

4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.

Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.

Проделав все по правилам, получаем результат:

Переносим под черту вниз последнюю цифру делимого — 8. В последний раз повторяем пункты алгоритма 2-4 и получаем:

В самой нижней строчке записываем число . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

Разделим натуральное число 7136 на натуральное число 9.

Запишем:

После второго, третьего и четвертого шага алгоритма запись примет вид:

Повторим цикл:

Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

Разделим число 7042035 на 7.

Ответ: 1006005

Деление чисел, оканчивающихся нулями

Решим устно примеры: 240 : 40, 720 : 80.

Заменим делитель произведением двух чисел: 40 = 4 ∙ 10, 80 = 8 ∙10.

240 : 40 = 240 : (4 ∙ 10) = 240 : 10 : 4 = 6

720 : 80 = 720 : (8 ∙10) = 720 : 10 : 8 = 9

Попробуем решить пример более сложный.

1560 : 60

Заменим 60 произведением 6 ∙ 10

1560 : 60 = 1560 : (6 ∙ 10) = 1560 :10 : 6 = 156 : 6

Затруднились?

Действительно, 156 разделить на 6 устно трудно. Значит, этот способ здесь не подходит!

Будем делить столбиком.

Теперь самостоятельно поработайте с  числами, которые оканчиваются  нулями. Устно выполняйте вычисления в первом столбике, письменно – во втором.

640 : 80 210 : 30

720 : 30 1280 : 80

Проверь себя.

640 : 80 = 640 : (8 ∙ 10) = 640 : 10 : 8 = 8 210 : 30 = 210 : (3 ∙ 10) = 210 : 10 : 3 = 7